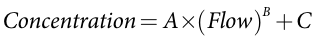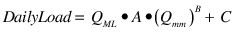Note: This is documentation for version 4.11 of Source. For a different version of Source, select the relevant space by using the Spaces menu in the toolbar above
Power function - SRG
The Power Function is a constituent generation model that fits a rating curve describing the relationship between constituent concentration or load and discharge. Two configuration options are available:
- a straight power curve, where Flow in ML/d has been used to generate a relationship with the solute concentration (mg/L); or
- a normalised power curve, where Flow in mm/d has been used to generate a relationship with the solute concentration (mg/L).
Scale
This model is a catchment scale model, but can be used at a regional scale if only applied to a single sub-catchment.
Principal developer
Cooperative Research Centre for Catchment Hydrology / eWater
Scientific Provenance
Widely used in modelling and discussed in the scientific literature. For example see Phillips (1999); Asselman (2000); Horowitz (2003).
Version
Source v4.3
Dependencies
The power function requires a spatial catchment configuration with Functional Units, and Lumped Constituents functionality enabled.
Availability/conditions
Power function is automatically installed with Source.
Flow phase
A common problem in hydrology and water quality investigations is the absence of water quality data to establish a relationship between solute concentration load and discharge. In the absence of actual sediment or solute concentration (SSC) data, the simplest and most basic analysis is to fit a smooth rating curve (or transport curve) to estimate sediment or solute concentrations for flux calculations. Although there are more than 20 methods for developing rating curves, the most common is a power function (regression) that relates SSC to water discharge, with the discharge measurement constituting the independent variable (eg. Phillips et al. 1999; Asselman 2000). This generally requires the log-transformation of SSC and discharge data prior to the analysis. The motivation for the use of such power functions includes their flexibility and their relative simplicity.
The Power Function (Equation 1) is fitted by adjusting the values of the parameters A, B and C to minimise the sum of the square of the residuals between the rating curve and observations. The units of concentration are mg/L, and the units of flow may be either ML/d or mm/d, depending on which form of the equation is being used..
| Equation 1 |
|---|
where:
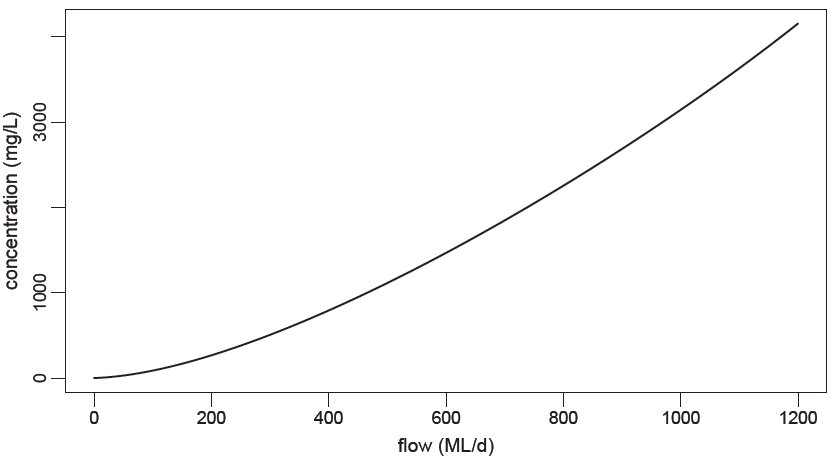
A the coefficient, represents the slope of the curve if plotted on semi-log axes.
B represents the "curvature" of the curve; B less than 1 means the curve is convex upwards, and B greater than 1 means the curve is concave upwards.
C represents the concentration at low flow.
Figure 1: Power Function
For B, values between 1.1 - 1.5 are common and a maximum value of 2 is recommended. |
Rating curves produce load estimates that are valid for the period over which the concentration samples were made (ie samples collected over 10 years means the rating curve will produce a reasonably accurate 10 year load estimate, but poorer annual, weekly and daily loads). |
Generating load time-series
The daily load time-series is calculated as the product of daily flow and the concentration at that flow (from the rating curve) for each FU. To ensure consistent units for this calculation, concentration from the rating curve (mg/L) is converted to kg/m3 (divide by 1,000). Daily flow (Q, ML/d) is converted to m3/d (multiply by 1,000), so that the product of daily flow and concentration provides load in kg/d. The final equation will be:
Equation 2 |
|---|
For the straight power curve function, flow in ML is dependent on the upstream sub-catchment area from which it has been derived or measured. Therefore, if the power function is to be applied in an adjacent sub-catchment the parameters for A, B and C need to be recalculated to reflect the new upstream sub-catchment area.
However, the power curve function that uses Flow in mm (Flow in ML divided by FU area in km2) to derive the A, B and C parameters can be applied to all FUs upstream of the node from which the flow and solute concentration has been measured. This configuration removes the dependency of area on the relationship derived between flow and solute concentration, as the flow calculated in mm at the end of a sub-catchment will be relative to the flow calculated at a FU.
Equation 3 |
|---|
where:
QML is in ML/d.
Qmm is in mm.
A is the slope of the curve of concentration vs runoff in mm.
Uncertainty in rating curves
Rating curves do not fully represent the variability in observed suspended sediment and solute concentrations, particularly at daily time-scales. Causes of unrepresented variability include:
|
Rating curves tend to under-predict concentrations at high flow, and over-predict concentrations at low flow. Therefore, the uncertainty in load is greater for shorter time periods, since the errors in high and low flow have less opportunity to average out (Horowitz, 2003). Rather than using rating curves to predict sediment load on a given day with accuracy, it is more appropriate to use them to predict load over months or years, or to construct concentration or load duration curves. Where concentration data are collected over >80% of the flow range, a study of data from a US monitoring site has shown that sediment rating curves can be used to generate reasonably accurate (15-20%) suspended sediment flux estimates for quarterly time-frames or longer, for large, medium and relatively small rivers (Horowitz, 2003). If samples are collected across the full range of hydrologic conditions, good estimates of the load for 5-year periods require as few as six samples per year, whereas good estimates of annual loads require as few as 12 samples per year (Horowitz, 2003). Of course, these recommendations are for predicting total load, which is delivered predominantly during flow events. Regular monitoring of low-flow concentrations may be important for other aspects of condition assessment. |
Input data
Values for parameters A, B and C and the maximum concentration of the constituent.
Using poor quality data to generate rating curves introduces uncertainty into rating curves. What is important is that the samples are collected across the range of flow rates. Reducing uncertainty in rating curves does not necessarily require long or extensive sampling records. Where concentration varies across the cross section due to gravitational and turbulence effects, taking concentration samples at the same point on the cross section (eg. automatic samplers) can bias the calculated sediment or solute load. This is particularly important at intermediate flows. |
Parameters or settings
The parameters for this model are summarised in Table 1.
Table 1. Model parameters
Parameter | Description | Units | Default | Min | Max |
|---|---|---|---|---|---|
A | Overall slope of the curve | 0 | 0 | ∞ | |
B | Curvature of the curve | 0 | 0 | 50 | |
C | Concentration at low flow | mg/L | 0 | 0 | 1000 |
Maximum concentration | Maximum concentration of sediment or solute | mg/L | 1000 | 0 | 1000 |
Output data
A time series of daily load in kg per time-step.
Configuration
None.
Reference list
Asselman, NEM 2000, ‘Fitting and interpretation of sediment rating curves’, Journal of Hydrology, vol. 234, pp. 228-248.
Horowitz, JA 2003, ‘An evaluation of sediment rating curves for estimating suspended sediment concentrations for subsequent flux calculations’, Hydrological Processes, vol. 177, pp. 3387-3409.
Phillips, JM, Webb, BW, Walling, DE & Leeks, GJL 1999, ‘Estimating the suspended sediment loads of rivers in the LOIS study area using infrequent samples’, Hydrological Processes, vol. 13, pp. 1035-1050.