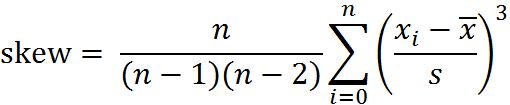Note: This is documentation for version 4.11 of Source. For a different version of Source, select the relevant space by using the Spaces menu in the toolbar above
Univariate Statistics SRG
Univariate statistics provide information on a single variable. They summarise and reveal patterns in that variable. In Source, the variable used to calculate statistics is a time series. Statistics are calculated in Results Manger on the Statistics tab, see Chart Statistics.
The types of univariate statistics available in Source are described in Table 1.
Table 1. Univariate Statistics
Statistic | Definition | Example for |
|---|---|---|
Minimum | Minimum value in the time series. | 0 |
Maximum | Maximum value in the time series. | 9 |
Number of Values | The number of values in the time series, not including nulls. | 6 |
Number of Nulls | The number of nulls, either missing values or values entered as -9999. These values are ignored in all other univariate statistics. | 1 |
Total | The sum of all values in the time series. | 27 |
Mean | The sum of all values in the time series divided by the number of values, | 5 |
Median | The middle value in the sorted list of all values in a time series. For n values, the middle value is . When n is even, the median is the mean of the two middle values. | 4 |
Standard Deviation | How widely values in the time series vary from the mean. See Standard Deviation. | 3.89 (to 2 decimal places) |
Skew | The skewness of the distribution of values in the time series. See Skew. | 0.23 (to 2 decimal places). |
Standard Deviation
Definition
The standard deviation (s) measures the amount by which values in the time series vary from the mean. It is defined as:
Equation 1 |
Where:
x is the value of time series x at time step i
is the mean of time series x
n is the number of values in time series x.
Interpretation
A low (smaller) standard deviation, indicates the values are close to the mean, with a narrow range; a high standard deviation indicates the values are spread out over a wider range.
Skew
Definition
The skew measures the degree of asymmetry of a distribution around its mean. It is defined as:
Equation 2 |
Where all terms are defined in Equation 1.
Interpretation
A symmetrical dataset will have a skew of 0. A positive skew indicates a distribution with an asymmetric tail extending toward values greater than the mean. Negative skew indicates a distribution with an asymmetric tail extending toward values less than the mean.